A pizza is a pizza, no matter how you slice it, right? Wrong.
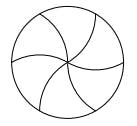
The mathematically inclined among us might want to ditch simple, straight lines organized around a central point for this cool curvy slice:
Joel Anthony Haddley and Steve Worsley
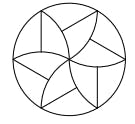
Got some more guests? No problem, just cut each piece in half:
Joel Anthony Haddley and Steve Worsley
The diagrams come from a new open-access math paper that, ostensibly, has something to do with pizza. In the introduction, the authors state,
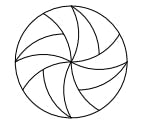
A tiling of a planar shape is called monohedral if all tiles are congruent to each other. We will investigate the possibility of producing monohedral tilings of the disk. Such tilings are produced on a daily basis by pizza chefs by taking radial cuts distributed evenly around the centre of the pizza. After constructing this tiling, a neighbourhood of the origin has non-trivial intersection with each tile. This brings us to the main question of this article: Can we construct monohedral tilings of the disk such that a neighbourhood of the origin has trivial intersection with at least one tile?
Don’t worry, it gets denser after that. To be honest, we at the Daily Dot have no clue what’s going on in this paper. Is this a guide for cutting pizza? A hypothetical math exercise? No idea. However, as the folks at Mashable pointed out, if this truly is a guide to pizza slicing, it’s a terrible one. You’re going to get some people who are just eating crust.
Joel Anthony Haddley and Steve Worsley
So maybe it’s not so great for pizza. But it is a great way to divide up a cinnamon roll.
Joel Anthony Haddley and Steve Worsley
H/T Mashable | Photo by Scott Bauer/Wikimedia (PD)
